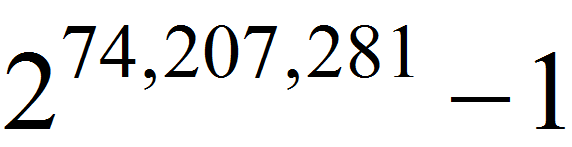 Πρώτοι αριθμοί είναι οι φυσικοί αριθμοί (μεγαλύτεροι του 1) που διαιρούνται μόνο με τον εαυτό τους και τη μονάδα, όπως οι 2, 3, 5, 7, 11, 13, κ.ο.κ.
Πρώτοι αριθμοί είναι οι φυσικοί αριθμοί (μεγαλύτεροι του 1) που διαιρούνται μόνο με τον εαυτό τους και τη μονάδα, όπως οι 2, 3, 5, 7, 11, 13, κ.ο.κ.
Οι πρώτοι αριθμοί που γράφονται στη μορφή 2ν-1, ονομάζονται πρώτοι του Mersenne, από το όνομα του Γάλλου μοναχού Marin Mersenne, τον πρώτο που διερεύνησε αριθμούς τέτοιες μορφής.
Το νέο ρεκόρ μεγαλύτερου πρώτου αριθμού επιτεύχθηκε πάλι από το πρόγραμμα GIMPS (Great Internet Mersenne Prime Search) το οποίο συνδέει χιλιάδες υπολογιστές στον κόσμο ψάχνοντας πρώτους αριθμούς.
Ένας υπολογιστής (του δικτύου GIMPS) στο Πανεπιστήμιο του Μισούρι στις ΗΠΑ κατέγραψε τον μεγαλύτερο μέχρι σήμερα πρώτο αριθμό, που γράφεται ως:
274,207,281-1 και ονομάζεται M74207281. Πρόκειται για το 49ο πρώτο του Mersenne.
Ο αριθμός αυτός αποτελείται από 22 338 618 ψηφία και είναι κατά 5 εκατομμύρια ψηφίαπερίπου μακρύτερος από τον προηγούμενο μεγαλύτερο γνωστό πρώτο αριθμό 257,885,161-1.
To Gimps ξεκίνησε πριν από 20 χρόνια και (παρά το «ατυχές» όνομά του) κατάφερε να ανακαλύψει τους 15 μεγαλύτερους γνωστούς μέχρι σήμερα πρώτους αριθμούς.
Επόμενος στόχος των ερευνητών είναι το βραβείο των 150 000 δολαρίων που προσφέρει το Electronic Frontier Foundation για την εύρεση πρώτου αριθμού με 100 εκατομμύρια ψηφία.
πηγή: https://www.mersenne.org

